Tüm Detaylarıyla Kriptografi Eğitimleri Doküman Eğitim
Anlatımını yapacağımız konu başlıkları aşağıdaki gibi olacaktır. Konu İçerik Başlıkları.
- 1. Kriptografi Giriş
- 2. Kriptosistem/Şifre Nedir?
- 3. Kriptografinin Tarihçesi (Şifrelerin Tarihi)
- 4. Modern Kriptanaliz
- 5. Kırılması Mümkün Olmayan Şifre: Tek Kullanımlı Şifre
- 6. Simetrik Kriptografi
- 7. Blok Şifreler
- 7.1 Feistel Yapı
- 7.2 Değişim Permütasyon Ağı
- 7.2.1 Anahtar ekleme katmanı (İng. key addition layer)
- 7.2.2 Değişim katmanı (İng. substitution layer)
- 7.2.3 Permütasyon katmanı (İng. diffusion layer)
- 8. Blok Şifre Çalışma Yöntemleri
- 8.1. CBC (Cipher Block Chaining)
- 8.2. CFB (Cipher Feedback)
- 8.3. OFB (Output Feedback)
- 8.4. CTR (Counter)
- 8.5. XTS: Genellikle tüm disk şifreleme işlemlerinde kullanılır.
- 9. Kaynakça
Sizlere bu konumuzda tüm detaylarıyla kriptografi üzerine geniş çaplı bir doküman hazırladık. Dokümanımızı anlamanız için elimizden geldiğince içerik başlıklara göre anlatımı yapmaya çalıştık. Görünürde uzun gibi olsada eğitim dokümanınızın içeriği, sonuna kadar okuyan arkadaşlarımız kazançlı çıkacaktır. 
1. Kriptografi Giriş
Kriptoloji (İng. cryptology) birçok güvenlik problemini çözen bir bilim dalıdır. Kısa ve eksik bir tanım vermek istersek, kriptolojiyi güvenli olmayan bir haberleşme kanalında güvenli haberleşmeyi sağlayan bilim dalı olarak tanımlayabiliriz. Bu alanda sıkça duyulan diğer iki terim ise kriptografi ve kriptanalizdir. Kriptografi (İng. cryptography) güvenli kriptosistem (İng. cryptosystem) ya da şifre (İng. cipher) tasarımıyla ilgilenir. Kriptanaliz (İng. cryptanalysis) ise bu kriptosistem ya da şifrelerin analiziyle ilgilenir. İyi bir şifre tasarlayabilmek için analiz etmeyi iyi bilmek gerekmektedir. Dolayısıyla kriptografi ve kriptanaliz birbirini besleyen iki farklı alandır. Günümüzde kriptografi kelimesi, kriptoloji kelimesiyle tamamen aynı anlamda kullanılmaktadır. Dolayısıyla kriptoloji ya da kriptografi kelimesinin hangisinin kullanılacağı tamamen bir tercih meselesidir. Türkçe'de bazen aynı anlamda kullanılsalar da bu noktada şifre ve parola kelimelerini ayırt etmemiz gerekir. Genellikle bir kullanıcı adıyla birlikte kullanılan gizli bilgiye parola (İng. password) denmektedir. Şifre ise gizlemek istediğimiz veriyi işleyerek başkaları tarafından anlaşılamayacak hale getiren ve daha sonra bu karmaşık veriyi eski haline döndüren şifreleme ve deşifreleme algoritmalarının bütününe verdiğimiz bir addır. Bu dokümanda kriptosistem ve şifre kelimeleri aynı anlamda kullanılmaktadır. Kriptografi günümüzde birçok güvenlik problemini çözmektedir. Bunlardan bazıları:
- Depolanan veri, mesaj ve görüşmelerin güvenliği
- Depolanan veri, mesaj ve görüşmelerinin bütünlüğünün korunması ve doğrulanması
- Kişi ve veri kimlik doğrulaması
- Yapılan işlemlerin inkâr edilememesi
Mevcut şifreleme algoritmaları depolanan verilerin, yollanan mesajların ya da herhangi bir yazılı, sesli, ya da görüntülü bir görüşmenin güvenliğini sağlayabilmektedir. Kriptografik özet fonksiyonları ve kimlik doğrulamalı şifreleme algoritmaları herhangi bir verinin içeriğinin değiştirilmediğini göstermekte kullanılabilmektedir. Açık anahtarlı kriptografi algoritmaları kimlik doğrulamayı sağlayabildiği gibi, benzer algoritmalar elektronik imza gibi uygulamalarda kullanılarak, yapılan bir işlemin sadece yetkili kişi ya da kişiler tarafından yapıldığını göstermektedir. Bu sayede yetkili kişiler daha sonra bu işlemi yaptıklarını inkâr edememektedir.
2. Kriptosistem/Şifre Nedir?
Korumak istediğimiz veriye düz metin (İng. plaintext) ismini veriyoruz. Düz metin, bilgisayarınızdaki bir dosya, yolladığınız bir SMS ya da Whatsapp mesajı, ya da bir GSM görüşmesi olabilir. Kısacası dijital veriye dönüştürülmüş her veriye düz metin diyebiliriz. Şifreleme algoritmalarına ihtiyacımız da bu noktada doğmaktadır. Düz metni, şifreli metin (İng. ciphertext) diyeceğimiz karmaşık bir hale getirip sadece bizim ya da yetki verdiğimiz başkalarının şifreli metinden düz metni elde edebileceği şifreleme algoritmalarına ihtiyaç duymaktayız. Düz metin olarak saklanan dosyalar USB bellek, harici disk ya da dizüstü bilgisayarlar çalındığında başkalarının eline geçecektir. Aynı şekilde düz metin kullanılarak yapılacak kablolu ya da kablosuz bütün görüşmeler, kullanılan haberleşme kanalını dinleyen herkes tarafından ele geçirilecektir. Özellikle kablosuz görüşmeleri dinlemek ve bunu yaparken de fark edilememek kablosuz haberleşmenin doğasından kaynaklanmaktadır. Bu noktada kriptografi, kullanılan haberleşme kanalının güvensiz olduğu varsayımıyla güvenlik sağlamaktadır. Dolayısıyla düz metni şifreli metne, şifreli metni de düz metne dönüştüren şifreleme ve deşifreleme algoritma ikilisine kriptosistem/şifre demekteyiz. Kriptografi bilimine aşina olmayanların yaptığı en büyük hata, çok karmaşık şifreleme yöntemleri tasarlayarak kimsenin bu yöntemleri keşfedemeyeceğini varsaymalarıdır ve bütün güvenliği bu algoritmanın gizliliğine dayandırmalarıdır. Anlaşılmazlık benimsenerek sağlanan bu güvenlik (İng. security by obscurity) hiçbir şekilde güvenlik sağlamamaktadır ve tasarımcıların tarih boyunca uyguladıkları bu yöntem her zaman hüsranla sonuçlanmıştır. Çoğu zaman tersine mühendislik yöntemleriyle kırılan bu sistemler, bazen de kriptografinin üç B’si olarak bilinen hırsızlık, şantaj ve rüşvet (İng. burglary, blackmail, bribery) yöntemleriyle kırılmaktadır. Bu durum her kriptograf tarafından bilinse de, kriptografi bilgisi olmayanlar hala hiçbir değeri olmayan bu tarz akademik makaleler yazmaya devam etmektedir. Yine benzeri bir şekilde milli algoritmaların gizli tutulması, uzmanlar tarafından yeterince analiz edilmemiş algoritmaların devlet sırlarını korumak için kullanılmasına neden olmaktadır. Bu tarz gizli tutulan şifrelerin güvenilir ve alanında uzman akademisyenlere analizlerinin yaptırılması son derece önemlidir. Şifreleme algoritmasını gizli tutmak, aynı zamanda bu algoritmanın uzmanlar tarafından yeterince analiz edilmesini de engellemektedir. Dolayısıyla bir şifrenin güvenliği hiçbir zaman algoritmanın gizli tutulmasına dayanmamalıdır. Bu durum genellikle Kerckhoffs Prensibi olarak bilinir.
Bir kriptosistem kullanılan gizli anahtar dışındaki her şeyi bilindiği halde güvenli olmalıdır. Örneğin günümüzde kullandığımız modern blok şifreler 128 bit yani 16 baytlık gizli anahtar kullanmaktadır ve şifrenin bütün yapısı akademik makalelerle ve uluslararası standartlarla herkesin ulaşımına açıktır.
3. Kriptografinin Tarihçesi (Şifrelerin Tarihi)
Şifrelerin Tarihi Tarihi şifreler genellikle kâğıt kalem kullanılarak uygulanan yöntemlerden oluşmaktadır. Şifrenin kendisi ve seçilecek gizli anahtar pratikte kullanılabilecek kadar kolay ve akılda tutulabilir olmalıdır. Çoğu eski şifreleme algoritması aslında harf değişim sistemleridir. Düz metin yazıldıktan sonra şifreleme algoritması ve gizli anahtar kullanılarak alfabedeki harfler başka harfler ile değiştirilir. Kelimeler arasındaki boşluklar ve noktalama işaretleri şifreli metine bakan birisinin düz metin hakkında bilgi elde etmesine neden olacağı için, boşluklar ve noktalama işaretleri şifreli metinden çıkartılır. Sezar Şifresi eski şifreleme algoritmalarına verilebilecek en basit örnektir. Eski Roma’da Julius Caesar tarafından keşfedildiği düşünülen ve aslında herhangi bir ilkokul öğrencisinin de tekrar keşfetmiş olabileceği bu yöntemde şifreli metin oluşturulurken düz metindeki her harf alfabede kendisinden 2 önce gelen harf ile değiştirilir. Burada 2 sayısı gizli anahtardır ve 29 harfli Türkçe alfabesi düşünüldüğünde gizli anahtar 28 farklı şekilde seçilebilir. Dolayısıyla şifreli metni ele geçiren birisi gizli anahtarı en kötü ihtimalle 28 denemede bulabilir. Dolayısıyla tasarlanacak şifrede seçilebilecek anahtar sayısının fazla olması gerekmektedir. Ne kadar fazla olacağı mevcut teknolojiye göre belirlenir ve ileriki bölümlerde açıklanacaktır.
Tekli harf değişimi şifreleme algoritmalarında anahtar sayısının çok büyük tutulabileceği en iyi örnek basit tek harfli değişim (İng. basic monoalphabetic substitution) yöntemidir. Bu yöntemde kullanılan alfabedeki harfler yan yana yazılır ve bu harflerin altına aynı alfabe bu sefer rastgele bir sırayla yazılır. Örneğin A harfinin altında T harfi varsa, şifreli metin için düz metindeki her A harfi T ile değiştirilir. Buradaki gizli anahtar rastgele yazdığımız harf dizilişidir ve 29 harfli Türkçe alfabesi için bu şifreleme yönteminde 29 faktöriyel değişik anahtar seçmek mümkündür.
Dolayısıyla şifreli metni ele geçiren kişi her anahtarı tek tek deneyebilecek teknolojik altyapıya sahip değildir.Kaba kuvvetle kırılmasının mümkün olmadığını söylediğimiz basit tek harfli değişim yöntemini dildeki tekrar kullanılarak kırmak son derece kolaydır. Eğer böyle olmasaydı bugün bile kullanılabilecek bir yöntem olurdu. Frekans analizi diye bilinen bu şifre kırma yöntemi bilinen en eski kriptanaliz yöntemlerinden birisidir. 9. yüzyılda Al-Kindi tarafından yazılan ve bilinen en eski kriptanaliz kitabi olan Kriptografik Mesajların Deşifrelenmesi Üzerine El Yazması (İng. A Manuscript on Deciphering Cryptographic Messages) kitabında frekans analizi yöntemi açıklanmaktadır. Bu kitabın bir kopyası Topkapı Müzesi’nde bulunmaktadır ve ücret karşılığı sayfalarının fotokopisini almak mümkündür.
4. Modern Kriptanaliz
Frekans analizi dildeki tekrara dayanmaktadır. Her dilde yapısı gereği bazı harfler diğerlerinden daha fazla kullanılmaktadır. Bir harfin hangi sıklıkla bir dilde yer aldığını ölçmenin en iyi yolu, o dilde yazılmış çok uzun bir yazı alıp her harfin kaç kez gözlemlendiğini saymaktır. Gözlemlenme sayısını dokümandaki bütün harflerin sayısına bölerek harflerin hangi olasılıkla o dilde yer aldığını hesaplayabiliriz. Bu olasılıklar dilden dile değişiklik göstermektedir. Örneğin İngilizcede en çok gözlemlenen harf E, daha sonra da T’dir. Dolayısıyla elde edilen şifreli metin yeterince uzunsa ve düz metin İngilizceyse, şifreli metindeki en çok gözlemlenen harfin E, ikinci en çok gözlemlenen harfin de T olma ihtimali çok yüksektir. Bu şekilde birkaç deneme yanılma ile düz metin tamamen ele geçirilebilir. Modern kriptanaliz tekniklerinin neredeyse tamamı istatistiksel yöntemler olduğu için, frekans analizi bilgisi günümüzde hala önemini korumaktadır. Mevcut tarayıcıların metin içinde arama özelliği kullanılarak çok uzun bir dokümanda hangi harfin kaç kez gözlemlendiğini görmek çok kolaydır. Ama hazır yazılımları kullanmak yerine kriptografi ve siber güvenlik alanında çalışanların kendi kodlarını yazması son derece önemlidir. Dolayısıyla bir dokümandaki harflerin ne sıklıkla gözlemlendiğini sayan bir kod yazmak iyi bir egzersizdir. Favori programlama dilinizde benzeri bir kod yazmak güzel bir egzersiz olacaktır. Frekans analizi ve benzeri yöntemlerle tek harfli değişim şifrelerini kırmak mümkün olduğu için, tarihte iki ya da daha fazla harfi aynı anda değiştiren yeni şifreler önerilmiştir. Bunlardan en meşhuru 1854’te Charles Wheatstone tarafından önerilen ve harf ikililerini değiştiren Playfair şifresidir. Birinci Dünya savaşı sırasında da kullanılan bu şifreyi mevcut bilgisayar kuvvetiyle kırmak son derece kolaydır. Mevcut bilgisayarların gücü sekiz harfli değişim şifrelerini bile kırmaya yeterli olacağı için, daha fazla harfi değiştiren şifrelere ihtiyaç vardır. Fakat bu tarz şifreleri kâğıt kalem kullanarak uygulamak pratik değildir. Bu gözlem, modern blok şifrelerin doğmasına neden olmuştur.
5. Kırılması Mümkün Olmayan Şifre: Tek Kullanımlı Şifre
Şifrelerle ilk tanışan insanların ilk merak ettiği soru, acaba kimsenin kıramayacağı bir şifre tasarlamanın mümkün olup olmadığıdır. Aslında kırılamaz şifre mümkündür: Tek Kullanımlı Şifre (İng. One-time pad). Fakat bu yöntem pratikte kullanımı son derece zor olduğu için nadiren kullanılmaktadır. Tek kullanımlı şifreyi kullanabilmek için düz metin bitler cinsinden yani sıfır ve birler olarak gösterilir. En az yollanacak düz metin uzunluğunda rastgele üretilmiş bir sıfır ve birler dizisinin (tek kullanımlık anahtar) önceden haberleşilecek kişiye güvenli bir yoldan ulaştırılması gerekmektedir. Şifreleme işlemi düz metin bitlerinin tek kullanımlık anahtarın bitleriyle ikilik tabanda toplamaktan ibarettir. Bu işlem XOR (exclusive OR) olarak bilinmektedir ve genellikle sembolü ile gösterilir. Şifreleme işlemine bir örnek aşağıdaki tabloda verilmiştir. Şifreli metni elde eden kişi, tek kullanımlık anahtar ile şifreli metni ikilik tabanda toplayarak düz metni geri elde edebilir.
Düz metin | 010101111001001... Tek kullanımlık anahtar | 101111010110101... Şifreli metin | 111010101111100...
Şifreli metin, düz metin hakkında hiçbir ipucu vermediği için bu yöntem kusursuz gizlilik sunmaktadır. İleride gerekli olması durumunda kullanılmak üzere oluşturulan tek kullanımlık anahtarların Washington ve Moskova arasında paylaşıldığı bilinmektedir. Fakat pratikte her mesaj için rastgele bir tek kullanımlık anahtar üretip haberleşilecek kişilere vermek mümkün olmadığı için modern kriptografik haberleşmede bu yöntemi kullanmamız mümkün değildir. Aynı anahtarı iki kez kullanmaksa sistemin kolaylıkla kırılmasına neden olmaktadır. Bu gözlemler akan şifrelerin doğmasına neden olmuştur. Akan şifrelerin mantığı 128 bit gibi kısa bir gizli anahtar kullanarak her haberleşme sırasında rastgele gözükecek tek kullanımlık anahtar dizisi üretmektir. Kâğıt kalem yöntemleri teknolojinin gelişmesiyle yerini önce Enigma gibi makinelere, daha sonra da dijital sistemlere bırakmıştır. Önceki bölümde anlatıldığı üzere dijital veri sıfır ve birlerle temsil edilmektedir. Dolayısıyla haberleşecek cihazlar önce kullanılacak alfabe üzerinde bir uzlaşıya varmalıdır. İngilizce’de encoding denen karakterlerin bitlerle olan gösterim şekli İngilizce ve benzeri dillerde genellikle ASCII tablosu kullanılarak yapılmaktadır. Türkçe gibi özel karakterler içeren Latin alfabesi kullanan diller genellikle UTF-8 benzeri genişletilmiş karakter listelerini kullanmaktadır.
6. Simetrik Kriptografi
Simetrik kriptografi ya da gizli anahtarlı kriptografi diye bilinen bu kategorideki algoritmalar, şifreleme ve deşifreleme işlemleri için aynı gizli anahtar bilgisinden faydalanmaktadır. Dolayısıyla güvenli haberleşmenin sağlanabilmesi için bu anahtar bilgisinin önceden güvenli bir şekilde haberleşecek kişi ya da cihazlar arasında paylaşılması gerekmektedir. Simetrik kriptografi alanındaki algoritmaları üç grupta toplayabiliriz:
A. Blok Şifre:
Blok şifrelerin temeli tarihi çoklu harf değişim şifrelerine dayanmaktadır. Bu algoritmalar 64 ya da 128 bit gibi kısa girdileri aynı uzunlukta çıktılar verecek şekilde şifreleyen yöntemlerdir. Bu boyuta blok uzunluğu denir. Dolayısıyla blok uzunluğundan daha büyük bir veri şifreleneceği zaman veri öncelikle blok uzunluğu boyutundaki bloklara bölünür. Şifreleme işlemi için günümüzde en az 128 bit uzunluğunda gizli anahtar kullanılmaktadır.
B. Akan Şifre:
Tek kullanımlık şifrenin sağladığı güvenliği sağlamayı hedefleyen bu yöntem 128 bit gibi kısa bir gizli anahtardan çok uzun ve rastgelelik özellikleri gösteren sıfır ve birlerden oluşan anahtar dizisi üretir. Şifreli metin düz metnin anahtar dizisiyle birleştirilmesiyle oluşturulur. Genellikle XOR işlemi kullanılır. Deşifreleme işlemi için gizli anahtar aynı şekilde kullanılarak yine aynı anahtar dizisi üretilir ve anahtar dizisi ile şifreli metin birleştirilerek düz metin geri elde edilir.
C. Mesaj Doğrulama Kodu:
Mesaj doğrulama kodları (İng. message authentication code (MAC)) bir şifreleme algoritması değildir. Bu algoritmalar şifrelenmeden gönderilen düz metnin haberleşme sırasında değiştirilmediğini ispatlamak için kullanılır. Gizli anahtar bilgisi kullanılarak düz metinden 128 bit gibi kısa bir etiket oluşturulur ve düz metin ile birlikte bu etiket de paylaşılır. Bu sayede gizli anahtara sahip herkes düz metinden etiket oluşturarak paylaşılan etiketin aynısını elde edip mesajı doğrulayabilir. Eğer bir nedenden ötürü düz metinde değişiklik, çıkarma ya da ekleme yapıldıysa, bu yeni düz metin bilgisi gizli anahtarla birlikte mesaj doğrulama kodu algoritmasına sokulduğunda oluşacak yeni etiket eskisinden farklı olacağı için, mesajın bütünlüğünün bozulduğu anlaşılacaktır.
7. Blok Şifreler.
Gündelik hayatta şifrelediğimiz veri kısa mesajlarımızdaki gibi birkaç bayt kadar çok kısa olabildiği gibi, bilgisayarımızdaki bir video dosyası gibi gigabaytları geçebilmektedir. Girdi boyutu bu kadar değişken olan bir algoritma tasarlamak kolay olmadığı için, blok şifreler 64 ya da 128 bit gibi çok kısa girdileri şifreleyecek şekilde tasarlanır. Bu blok uzunluğundan daha uzun veri bloklara bölünür ve verinin tamamının nasıl şifreleneceği kullanılacak olan çalışma yöntemi (İng. mode of operation) ile belirlenir. Dolayısıyla bir düz metin, aynı şifreleme algoritması ama farklı çalışma yöntemleri kullanılarak şifrelenirse elde edilecek şifreli metinler birbirinden çok farklı olacaktır. Özetlemek gerekirse,
- Blok şifreler b bit uzunluğundaki veri üzerinde çalışır,
- Düz metin b bit uzunluğundaki bloklara bölünür,
- Her blok k bit uzunluğundaki anahtar yardımıyla şifrelenerek yine b bit uzunluğunda çıktı oluşturur,
- Çıktı bloklarından şifreli metin elde edilir, şifreleme sırasında bloklar arasında ne tür bir ilişki kurulacağı seçilen çalışma yöntemine göre belirlenir.
Modern blok şifreler blok uzunluğunu 64 bit ya da 128 bit seçmektedir. Bazı hafif şifreler 32 bit gibi daha kısa blok uzunluğu kullanmaktadır ama bu tarz kısa blok şifreler aynı gizli anahtar ile uzun süre kullanılırsa, trafiği dinleyerek çok fazla şifreli metin elde edecek birisi tarafından kırılmaya müsait hale gelebilir. Dolayısıyla bu kadar kısa blok şifreler ya haberleşmenin nadiren yapıldığı durumlarda ya da gizli anahtarın belirli kısa aralıklarla değiştirildiği durumlarda kullanılmalıdır. Günümüz teknolojisinde 128 bit anahtar kişisel güvenlik için yeterlidir. Çok uzun yıllar güvenliğin korunması istendiği durumlarda 256 bit anahtar tercih edilmelidir. Bazı basit tasarımlar 64 ya da 80 bit gibi kısa anahtarların kullanılmasına izin verse de bu şifreler herhangi bir güvenlik sunmamaktadır. Bilgi teorisinin (İng. information theory) babası sayılan Claude Shannon (1916-2001) 1949 yılında yayınladığı makalesinde şifre tasarımı için çok önemli iki fikir sunmuştur: Karmaşa (İng. confusion) ve yayılım (İng. diffusion). Karmaşa, şifreli metnin düz metin ve gizli anahtara çok karmaşık bir istatistikle bağlı olması ve dolayısıyla kriptanalizcinin bu ilişkiden faydalanamayacağı anlamına gelmektedir. Yayılım ise düz metin ve gizli anahtarın her bitinin şifreli metnin çok fazla sayıda bitini etkilemesi olarak düşünülebilir. Ne yazık ki karmaşa ve yayılım fikirleri ölçülebilir, somut kavramlar değildir. Dolayısıyla şifre tasarımında kullanılan fonksiyonlar, değerler ve seçimler bazı matematiksel temellere dayandırılır ve bilinen kriptanaliz yöntemlerine karşı dayanıklılıkları test edilir. Fakat bu tasarımlar henüz keşfedilmemiş kriptanaliz tekniklerine karşı dayanıksız olabilirler. Dolayısıyla blok şifre güvenliği her zaman bilinen yöntemlere karşı güvenlik şeklinde yorumlanmalıdır.
Bir blok şifre birçok karmaşık operasyon kullanılarak tasarlanabilir. Fakat bu tarz bir yaklaşım uygulama aşamasında zorluklar çıkartabileceği gibi, kriptanalizcinin de analizini zorlaştıracaktır. Dolayısıyla bunun yerine döngü (İng. round) ismi verilen bir fonksiyonun tasarlanıp bunun art arda r kez kullanılması modern blok şifre tasarımında kullanılan bir yöntemdir. Bir döngü içerisinde karmaşa ve yayılımı sağlayacak işlemlerin yanı sıra, aynı zamanda gizli anahtarın da bir kısmı ya da tamamı kullanılır.
Gizli anahtar bilgisinin her döngüde aynı şekilde kullanılması bazı tasarımlarda güvenlik açığı yaratabileceği için gizli anahtar o blok şifre için tasarlanmış anahtar kullanımı (İng. key schedule) algoritmasına sokulur ve her döngüde kullanılacak döngü anahtarları oluşturulur. Çoğu blok şifre tasarımı genellikle iki kategoride değerlendirilebilir: Değişim permütasyon ağı (İng. substitution permutation network) ve Feistel yapı (İng. Feistel structure).
7.1 FEİSTEL YAPI
Horst Feistel (1915-1990) tarafından önerilen bu metotta girdi sağ ve sol olmak üzere iki parçaya ayrılır. Döngü fonksiyonu bir parçayı işleme sokarak çıktıyı diğer parçayla işleme sokar. Bu sayede iki parçanın biri değişime uğramış olur. Ardından sağ ve sol parçaların yeri değiştirilir. Bu sayede her döngüde bir önceki döngüde etkilenmemiş parça değişime uğrar.  Döngü fonksiyonu anahtar ekleme kısmını içerdiği gibi, karmaşa ve yayılımı sağlayacak değişim ve permütasyon katmanları içermektedir (yandaki figürü inceleyiniz). Genelleştirilmiş Feistel yapılarda girdi iki yerine dört ya da sekiz gibi daha fazla sayıda parçalara bölünür. Feistel şifrelere verilebilecek en bilinen örnek DES (Data Encryption Standard) blok şifresidir. 1970’lerde IBM tarafından yapılan bu tasarım 1976’da NSA’in üzerinde bazı değişiklikler yapmasından sonra standartlaşmıştır. Blok uzunluğu 64 bit, anahtar uzunluğu 56 bit ve döngü sayısı 16’dır. 56 bit anahtar çok kısa olduğu için 1990’larda kaba kuvvet saldırılarına yenik düşmüştür. Bu kısa anahtar problemini çözmek için DES’i üç kez üst üste farklı üç anahtar ile kullanan 3DES (Triple DES) algoritması önerilmiştir. Bu şifreleme algoritması 112 bitlik güvenlik sunmaktadır ve Türkiye’deki birçok temassız kredi kartı 3DES algoritması kullanmaktadır. 3DES algoritması hala Amerikan standartlarında tavsiye edilen algoritmalar arasında yer almaktadır.
Döngü fonksiyonu anahtar ekleme kısmını içerdiği gibi, karmaşa ve yayılımı sağlayacak değişim ve permütasyon katmanları içermektedir (yandaki figürü inceleyiniz). Genelleştirilmiş Feistel yapılarda girdi iki yerine dört ya da sekiz gibi daha fazla sayıda parçalara bölünür. Feistel şifrelere verilebilecek en bilinen örnek DES (Data Encryption Standard) blok şifresidir. 1970’lerde IBM tarafından yapılan bu tasarım 1976’da NSA’in üzerinde bazı değişiklikler yapmasından sonra standartlaşmıştır. Blok uzunluğu 64 bit, anahtar uzunluğu 56 bit ve döngü sayısı 16’dır. 56 bit anahtar çok kısa olduğu için 1990’larda kaba kuvvet saldırılarına yenik düşmüştür. Bu kısa anahtar problemini çözmek için DES’i üç kez üst üste farklı üç anahtar ile kullanan 3DES (Triple DES) algoritması önerilmiştir. Bu şifreleme algoritması 112 bitlik güvenlik sunmaktadır ve Türkiye’deki birçok temassız kredi kartı 3DES algoritması kullanmaktadır. 3DES algoritması hala Amerikan standartlarında tavsiye edilen algoritmalar arasında yer almaktadır.
7.2 DEĞİŞİM PERMÜTASYON AĞI
Bu yapıda oluşturulan blok şifrelerde bir döngü genellikle üç katmandan oluşur (figürü inceleyiniz).
7.2.1 Anahtar ekleme katmanı (İng. key addition layer):
Döngü anahtarı girdi ile işleme sokulur. Genellikle XOR ya da modüler toplama gibi basit bir işlemden oluşmaktadır.
7.2.2 Değişim katmanı (İng. substitution layer):
Bu katman karmaşa sağlamak için kullanılır. Genellikle modüler toplama işlemi ya da değişim kutuları (İng. substitution box (S-box)) gibi küçük boyuttaki girdileri değiştiren önceden seçilmiş tablo değerleri kullanılır.
7.2.3 Permütasyon katmanı (İng. diffusion layer):
Bu katman dağılımı sağlar. Bitlerin yerlerinin değiştirilmesi, bitlerin kaydırılması, matris çarpımı gibi lineer işlemler kullanılır. 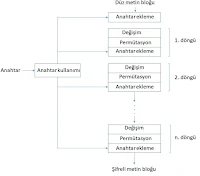 Figürde görüldüğü üzere algoritmanın ilk ve son aşaması anahtar bilgisinin işleme sokulmasını içermektedir. Bu sayede şifreleme algoritmasının bütün detaylarını bilen ve bir şifreli metin ya da düz metin ele geçiren saldırgan, gizli anahtarı bilmediği için bu anahtar ekleme katmanlarını aşamayacaktır. Dolayısıyla iç katmanlardaki herhangi bir bilgiyi ele geçiremeyecek ve dolayısıyla da gizli anahtar hakkında bilgi elde edemeyecektir. Bütün dünyada en çok kullanılan şifreleme algoritması olan AES ve hafif kriptografik uygulamalar için ISO/IEC standardı olan PRESENT blok şifreleri, değişim permütasyon ağı kullanılarak oluşturulan blok şifrelere örnektir. PRESENT şifresi düşük kapasiteli cihazlar için tasarlanmıştır, bu yüzden yapısı son derece basittir.
Figürde görüldüğü üzere algoritmanın ilk ve son aşaması anahtar bilgisinin işleme sokulmasını içermektedir. Bu sayede şifreleme algoritmasının bütün detaylarını bilen ve bir şifreli metin ya da düz metin ele geçiren saldırgan, gizli anahtarı bilmediği için bu anahtar ekleme katmanlarını aşamayacaktır. Dolayısıyla iç katmanlardaki herhangi bir bilgiyi ele geçiremeyecek ve dolayısıyla da gizli anahtar hakkında bilgi elde edemeyecektir. Bütün dünyada en çok kullanılan şifreleme algoritması olan AES ve hafif kriptografik uygulamalar için ISO/IEC standardı olan PRESENT blok şifreleri, değişim permütasyon ağı kullanılarak oluşturulan blok şifrelere örnektir. PRESENT şifresi düşük kapasiteli cihazlar için tasarlanmıştır, bu yüzden yapısı son derece basittir. 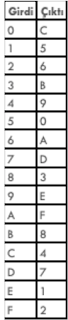 Blok uzunluğu 64 bit, anahtar uzunluğu 80 ya da 128 bit ve döngü sayısı 31 olan bu blok şifrenin iki döngüsü aşağıdaki figürde gösterilmiştir. Bu figürde her çizgi tek bir bitlik bilgiye denk gelmektedir. Anahtar kullanımı algoritması her döngü için 64 bitlik döngü anahtarları üretmekte ve anahtar ekleme katmanında 64 bitlik döngü girdisi o döngü anahtarıyla XOR işlemine sokulmaktadır. Figürde görüldüğü üzere değişim katmanında her 4 biti farklı bir 4 bit ile değiştiren bir değişim kutusu kullanılmıştır. Bu tarz değişim kutuları genellikle 16’lık tabanda yazılmış bir tablo ile gösterilir. PRESENT şifresi için seçilen değişim kutusu yandaki tabloda verilmiştir. Permütasyon katmanındaysa sadece bitlerin yeri değiştirilmektedir. PRESENT kullanıcılara 80 ya da 128 bit anahtar seçme imkanı sunsa da 80 yerine 128 bit anahtar seçmek ihmal edilebilecek kadar küçük bir performans farkı yarattığı için bu blok şifre hiçbir zaman 80 bit anahtar ile kullanılmamalıdır. Dünyada en çok kullanılan şifreleme algoritması şüphesiz ki AES (Advanced Encryption Standard) blok şifresidir. DES blok şifresinin 1990’larda kırılabilir hale gelmesi nedeniyle 2001 yılında Amerikan Ulusal Standart ve Teknoloji Enstitüsü herkesin katılımına açık bir yarışma hazırlamış ve yarışmanın kazananı Rijndael blok şifresi AES ismiyle standartlaştırılmıştır. Belçikalı Joan Daemen ve Vincent Rijmen tarafından tasarlanan bu blok şifre henüz kırılamamıştır ve Snowden dokümanları da Amerikan istihbaratının bu şifreyi kıramadığını göstermektedir. AES blok şifresi 128 bit blok uzunluğuna sahiptir. 128, 192 ve 256 bit anahtar uzunluğunu destekleyen bu blok şifrenin döngü sayısı da anahtar uzunluğuna göre 10, 12 ya da 14 olmaktadır.
Blok uzunluğu 64 bit, anahtar uzunluğu 80 ya da 128 bit ve döngü sayısı 31 olan bu blok şifrenin iki döngüsü aşağıdaki figürde gösterilmiştir. Bu figürde her çizgi tek bir bitlik bilgiye denk gelmektedir. Anahtar kullanımı algoritması her döngü için 64 bitlik döngü anahtarları üretmekte ve anahtar ekleme katmanında 64 bitlik döngü girdisi o döngü anahtarıyla XOR işlemine sokulmaktadır. Figürde görüldüğü üzere değişim katmanında her 4 biti farklı bir 4 bit ile değiştiren bir değişim kutusu kullanılmıştır. Bu tarz değişim kutuları genellikle 16’lık tabanda yazılmış bir tablo ile gösterilir. PRESENT şifresi için seçilen değişim kutusu yandaki tabloda verilmiştir. Permütasyon katmanındaysa sadece bitlerin yeri değiştirilmektedir. PRESENT kullanıcılara 80 ya da 128 bit anahtar seçme imkanı sunsa da 80 yerine 128 bit anahtar seçmek ihmal edilebilecek kadar küçük bir performans farkı yarattığı için bu blok şifre hiçbir zaman 80 bit anahtar ile kullanılmamalıdır. Dünyada en çok kullanılan şifreleme algoritması şüphesiz ki AES (Advanced Encryption Standard) blok şifresidir. DES blok şifresinin 1990’larda kırılabilir hale gelmesi nedeniyle 2001 yılında Amerikan Ulusal Standart ve Teknoloji Enstitüsü herkesin katılımına açık bir yarışma hazırlamış ve yarışmanın kazananı Rijndael blok şifresi AES ismiyle standartlaştırılmıştır. Belçikalı Joan Daemen ve Vincent Rijmen tarafından tasarlanan bu blok şifre henüz kırılamamıştır ve Snowden dokümanları da Amerikan istihbaratının bu şifreyi kıramadığını göstermektedir. AES blok şifresi 128 bit blok uzunluğuna sahiptir. 128, 192 ve 256 bit anahtar uzunluğunu destekleyen bu blok şifrenin döngü sayısı da anahtar uzunluğuna göre 10, 12 ya da 14 olmaktadır.  Şifreleme algoritmalarında anahtar uzunluğu mevcut atak türlerine ve mevcut teknolojiye göre seçilmektedir. Örneğin bir simetrik şifreleme algoritmasına ait düz metin ve ona karşılık gelen şifreli metin elde edilirse, saldırgan düz metni her anahtarla şifreleyip, çıkan şifreli metin kendi ele geçirdiği şifreli metin ile aynı mı diye kontrol ederek gizli anahtarı bulabilir. Böyle bir saldırıyı gerçekleştirebilmek için k bitlik gizli anahtar kullanan bir şifreleme algoritması için en fazla 2 üssü k adet şifreleme işlemi yapmak gerekmektedir. Dolayısıyla k değerini bir arttırmak, saldırganın işini iki kat zorlaştırmak anlamına gelmektedir.
Şifreleme algoritmalarında anahtar uzunluğu mevcut atak türlerine ve mevcut teknolojiye göre seçilmektedir. Örneğin bir simetrik şifreleme algoritmasına ait düz metin ve ona karşılık gelen şifreli metin elde edilirse, saldırgan düz metni her anahtarla şifreleyip, çıkan şifreli metin kendi ele geçirdiği şifreli metin ile aynı mı diye kontrol ederek gizli anahtarı bulabilir. Böyle bir saldırıyı gerçekleştirebilmek için k bitlik gizli anahtar kullanan bir şifreleme algoritması için en fazla 2 üssü k adet şifreleme işlemi yapmak gerekmektedir. Dolayısıyla k değerini bir arttırmak, saldırganın işini iki kat zorlaştırmak anlamına gelmektedir.
Aşağıdaki tabloda da görüleceği üzere k değerindeki artış saldırganın işini üstel şekilde zorlaştırmaktadır. Yazdığımız en iyi yazılımlar sayesinde AES için CPU kullanarak saniyede 2 üssü 24 adet anahtar, ekran kartları kullanarak ise 2 üssü 33 adet anahtar deneyebiliyoruz.
Bir yılda 2 üssü 27’den daha az saniye olduğu düşünülürse, dünyadaki bütün işlem kapasitesine sahip cihazları kullansak bile 128 bit anahtarlı bir şifreyi kırmadan önce evrenin sonu gelecektir. 
8. Blok Şifre Çalışma Yöntemleri
Blok şifre algoritmaları incelendiğinde iki problem karşımıza çıkıyor:
- Eğer düz metin boyutu blok şifrenin blok uzunluğundan fazlaysa, birden fazla blok nasıl şifrelenmelidir?
- Eğer düz metin uzunluğu blok uzunluğunun herhangi bir katı değilse, kalan boşluklar nasıl şifrelenip deşifrelenmelidir?
Birinci sorunun basit bir çözümü düz metni bloklara bölüp, her bloğu ayrı ayrı şifreleyip çıkan şifreli metin bloklarını uç uca ekleyerek şifreli metni elde etmektir. Bu yapı aşağıdaki figürde gösterilmiştir. Düz metin blokları Pi, şifreli metin blokları Ci, gizli anahtar k ile gösterilmiştir.  Akla gelen ilk çözüm bu olsa da ve kriptografi alanında bilgi sahibi olmayanlar tarafından sürekli kullanılsa da bu yöntem kriptografik açıdan hiçbir güvenlik sunmamaktadır ve asla kullanılmamalıdır. Electronic Codebook (ECB) çalışma yöntemi olarak bilinen bu yöntemin problemi aynı düz metin bloğunun aynı şifreli metin bloğunu oluşturmasıdır. Bu durumun oluşturacağı sıkıntıyı BMP formatındaki resim dosyalarını şifreleyerek görmek çok kolaydır.
Akla gelen ilk çözüm bu olsa da ve kriptografi alanında bilgi sahibi olmayanlar tarafından sürekli kullanılsa da bu yöntem kriptografik açıdan hiçbir güvenlik sunmamaktadır ve asla kullanılmamalıdır. Electronic Codebook (ECB) çalışma yöntemi olarak bilinen bu yöntemin problemi aynı düz metin bloğunun aynı şifreli metin bloğunu oluşturmasıdır. Bu durumun oluşturacağı sıkıntıyı BMP formatındaki resim dosyalarını şifreleyerek görmek çok kolaydır.  Yandaki figürlerde şifrelenmemiş ODTÜ logosunun ve aynı logonun AES blok şifresinin ECB çalışma yöntemiyle şifrelenmiş hali gösterilmiştir. Şifreli metne bakarak düz metnin ne olduğu hemen anlaşılmaktadır.
Yandaki figürlerde şifrelenmemiş ODTÜ logosunun ve aynı logonun AES blok şifresinin ECB çalışma yöntemiyle şifrelenmiş hali gösterilmiştir. Şifreli metne bakarak düz metnin ne olduğu hemen anlaşılmaktadır.  Amerikan Ulusal İstatistik ve Standartlar Enstitüsü (NIST) tarafından tavsiye edilen çalışma yöntemleri aşağıdaki gibi olacak. Anlatımını yapacağımız blok şifrelemelerine ait alt başlıklarımız; CBC (Cipher Block Chaining), 8.2. CFB (Cipher Feedback), OFB (Output Feedback), CTR (Counter) ve XTS olmak üzere beş alt başlık dizininde sizlere anlatımını yaparak konumuza devam edelim. Yeri gelmişken belirtmekte fayda olacağını düşünerek ek bir not bilgisi verelim. Sitemizde daha önce açılmış Kriptografi Eğitimlerine yönelik diğer konularımıza bakmanız, sizlere çok büyük fayda sağlayacaktır. Konuyla ilgili sorularınızı yorum bölümünden dile getirebilirsiniz veya iletişime geçebilirsiniz. Konumuza devam edecek olursak.
Amerikan Ulusal İstatistik ve Standartlar Enstitüsü (NIST) tarafından tavsiye edilen çalışma yöntemleri aşağıdaki gibi olacak. Anlatımını yapacağımız blok şifrelemelerine ait alt başlıklarımız; CBC (Cipher Block Chaining), 8.2. CFB (Cipher Feedback), OFB (Output Feedback), CTR (Counter) ve XTS olmak üzere beş alt başlık dizininde sizlere anlatımını yaparak konumuza devam edelim. Yeri gelmişken belirtmekte fayda olacağını düşünerek ek bir not bilgisi verelim. Sitemizde daha önce açılmış Kriptografi Eğitimlerine yönelik diğer konularımıza bakmanız, sizlere çok büyük fayda sağlayacaktır. Konuyla ilgili sorularınızı yorum bölümünden dile getirebilirsiniz veya iletişime geçebilirsiniz. Konumuza devam edecek olursak.
8.1 CBC (Cipher Block Chaining):
ECB çalışma yöntemindeki zafiyeti gidermek için bu yöntemde her şifreli metin bloğu, bir sonraki düz metin bloğuyla XOR’lanır. Bu sayede aynı iki düz metin bloğu farklı şifreli metin bloğu oluşturmaktadır. İlk düz metin bloğundan önce bir şifreli metin bloğu olmadığı için, başlangıç vektörü (İng. initialization vector (IV)) denen ve ne olduğu standartlardan öğrenilebilecek bir değer ilk düz metin bloğuyla XOR’lanır. Birçok yerde tercih edilen bu yöntemin dezavantajı şifreleme işleminin paralelleştirilemiyor olmasıdır. Çünkü bir bloğu şifreleyebilmek için o bloktan önceki blokların hepsinin şifrelenmiş olması gerekmektedir. Bu yöntem için şifreleme ve deşifreleme işlemlerinin nasıl yapılacağı aşağıdaki iki figürde gösterilmiştir. 

8.2 CFB (Cipher Feedback)
8.3 OFB (Output Feedback)
8.4 CTR (Counter)Sayaç
CTR (Counter)Sayaç ismi verilen bu yöntemde düz metni şifrelemek yerine, gizli olmayan sayaç bilgisi şifrelenir ve sonrasında çıktı düz metin bloğuyla XOR’lanır. Eğer birden fazla düz metin bloğu varsa, her yeni blok için sayacın değeri bir arttırılır. Aynı sayaç farklı şifreleme işlemlerinde kullanılırsa bu yöntemi kırmak mümkün olduğu için, genellikle sayacın başına sadece o görüşmede kullanılmak üzere rastgele üretilmiş bir sayı eklenir. Bu tek kullanımlık değere kriptografide nonce adı verilir. Diğer yöntemlere kıyasla birçok artısı olan bu yöntem mevcut iOS ve Android işletim sistemlerinde tüm diskin şifrelenmesinde de kullanılmaktadır. Bu yöntem için şifreleme ve deşifreleme işlemlerinin nasıl yapılacağı aşağıdaki iki figürde gösterilmiştir. 

8.5 XTS: Genellikle tüm disk şifreleme işlemlerinde kullanılır.
ECB yönteminin zafiyeti, yukarıda önerdiğimiz çalışma yöntemlerinde bulunmamaktadır. O örnekte kullandığımız ODTÜ logosunu aşağıdaki figürde yine AES blok şifresiyle ama bu sefer Sayaç çalışma yöntemiyle şifreledik. ODTÜ logosu ve AES blok şifresinin Sayaç çalışma yönteminde kullanılmasıyla elde edilen şifreli metne bakarak düz metin hakkında bilgi elde etmek mümkün değildir. 
 Artık ikinci sorumuzun cevabını verebiliriz: Eğer düz metin uzunluğu blok uzunluğunun herhangi bir katı değilse, kalan boşluklar nasıl şifrelenip deşifrelenmelidir? Örneğin 2 bayt yani 16 bit şifreleyeceksek ve kullanacağımız blok şifrenin blok boyutu 64 bitse, kalan 48 biti ne şekilde seçmeliyiz? Akla ilk gelen yöntem o bitleri sıfır seçmek olacaktır. Ama bu durum, deşifreleme işlemi yapan kişi için bir şüphe oluşturacaktır. Deşifreleme işlemi bittiğinde o sıfır olan 48 bit acaba düz metnin bir parçası mı yoksa kalan boş bitler midir? Deşifreleme işlemini yapan kişinin bu sorunun cevabını vermesi mümkün değildir. Dolayısıyla bu boş kalan bitleri özel bir kalıba göre doldurursak, deşifreleme işlemini yapan kişi de bu kalıbı bileceği için deşifreleme işleminden sonra o bitleri silebilir. Bu işleme dolgu (İng. padding) denmektedir ve standartlarda ve literatürde tavsiye edilen yöntem bir adet 1 biti ve geriye kalan bitleri 0 biti ile doldurmaktır. Örneğin şifreleyeceğimiz 16 bit 1111101010110001 ise, dolgudan sonra bu blok aşağıdaki şekle dönüşecektir (dolgu bitleri kalın yazı türüyle gösterilmiştir).
Artık ikinci sorumuzun cevabını verebiliriz: Eğer düz metin uzunluğu blok uzunluğunun herhangi bir katı değilse, kalan boşluklar nasıl şifrelenip deşifrelenmelidir? Örneğin 2 bayt yani 16 bit şifreleyeceksek ve kullanacağımız blok şifrenin blok boyutu 64 bitse, kalan 48 biti ne şekilde seçmeliyiz? Akla ilk gelen yöntem o bitleri sıfır seçmek olacaktır. Ama bu durum, deşifreleme işlemi yapan kişi için bir şüphe oluşturacaktır. Deşifreleme işlemi bittiğinde o sıfır olan 48 bit acaba düz metnin bir parçası mı yoksa kalan boş bitler midir? Deşifreleme işlemini yapan kişinin bu sorunun cevabını vermesi mümkün değildir. Dolayısıyla bu boş kalan bitleri özel bir kalıba göre doldurursak, deşifreleme işlemini yapan kişi de bu kalıbı bileceği için deşifreleme işleminden sonra o bitleri silebilir. Bu işleme dolgu (İng. padding) denmektedir ve standartlarda ve literatürde tavsiye edilen yöntem bir adet 1 biti ve geriye kalan bitleri 0 biti ile doldurmaktır. Örneğin şifreleyeceğimiz 16 bit 1111101010110001 ise, dolgudan sonra bu blok aşağıdaki şekle dönüşecektir (dolgu bitleri kalın yazı türüyle gösterilmiştir).
1111101010110001100000000000000000000000000000000000000000000000
Deşifreleme işlemi yapan kişi en sağdaki bütün sıfırları ve göreceği ilk 1 bitini sileceği için doğru düz metne ulaşacaktır. Bu noktada yeni bir problem daha ortaya çıkıyor: Eğer düz metin, blok uzunluğunun bir katıysa dolgu nasıl yapılmalıdır? Eğer bu durumda dolgu yapmazsak, bu sefer deşifreleme işlemini yapan kişi sondaki sıfırları ve ilk 1 bitini dolgu zannedebilir. Dolayısıyla bu yanlış anlaşılmayı engellemek için, eğer düz metin blok uzunluğunun bir katıysa, dolgu olarak yepyeni bir blok daha eklenir.
1000000000000000000000000000000000000000000000000000000000000000
